/opracował dr hab. Tadeusz Szumiata, prof. UTH Radom/

Dlaczego stary wzorzec masy jest zbyt stary?

Wzorzec kilograma, jako ostatni w całym międzynarodowym układzie miar SI, opierał się na artefakcie. Był nim walec z platyny i irydu (90% Pt i 10% Ir) o wysokości równej średnicy wynoszącej ok. 39 mm. Nadano mu dostojną nazwę Le Grand K („Wielki K”). Wzorzec ten przechowywany był w Międzynarodowym Biurze Miar BIPM (Bureau International des Poids et Mesures) w Sèvres pod Paryżem i obowiązywał od września 1889 roku, na mocy decyzji I Generalnej Konferencji Miar (Conférence Générale des Poids et Mesures, CGPM). Przez dziesięciolecia nauka i technologia rozwijały się oraz rewolucjonizowały metrologię różnych wielkości fizycznych, ale wzorzec kilograma pozostawał bez zmian. Brakowało racjonalnych pomysłów na zmiany wzorca masy, jednak w końcu okazało się, że Le Grand K zaczął wykazywać odmienne trendy długoczasowych zmian masy w stosunku do kopii porównawczych. Przyczyną tych zmian były trudne do monitorowania zjawiska utraty lub absorbcji atomów na powierzchni poszczególnych wzorców.

Rys. 1. Replika dotychczasowego międzynarodowego wzorca masy (Le Grand K) w Sèvres pod Paryżem https://en.wikipedia.org/wiki/International_Prototype_of_the_Kilogram#/media/File:Prototype_kilogram_replica.JPG

Jak podało najbardziej prestiżowe czasopismo naukowe na świecie, NATURE [1], na przestrzeni stulecia różnica masy pomiędzy nadrzędnym wzorcem (Le Grand K) a kopiami referencyjnymi wyniosła aż 50 mikrogramów (Rys. 2).

Rys. 2. Zmiany długoczasowe masy wtórnych wzorców międzynarodowych i narodowych w stosunku do nadrzędnego wzorca masy (Le Grand K) opublikowane w NATURE [1] https://www.nature.com/articles/d41586-018-07424-8

Stanowiło to poważny sygnał ostrzegawczy, ale zarazem silną motywację do pracy nad innowacyjnym wzorcem kilograma opartym nie na obiekcie materialnym, lecz na zjawiskach i stałych fizycznych. Pierwsze rekomendacje w tym zakresie sformułowała 23. Generalna Konferencja Miar CGPM w 2007 roku i CCM BIPM (Consultative Committee for Mass and Related Quantities) w 2010 roku. Jednak prawdziwą rewolucję w metrologii masy i całym układzie miar SI przyniosły lata 2018 i 2019.

Na czym polega rewolucja w międzynarodowym układzie jednostek SI?

Przedstawiciele narodowych instytucji metrologicznych z całego świata uczestniczący w 26 Conférence Générale des Poids et Mesures (CGPM) w Wersalu jesienią 2018 roku zadecydowali w demokratycznym głosowaniu, że układ SI zostanie oparty na ustalonych wartościach liczbowych zbioru siedmiu stałych fizycznych, na podstawie których będą wyprowadzone definicje siedmiu jednostek podstawowych SI (Rys. 3). Niniejsza zmiana uprawomocniła się 20 maja 2019 roku.

Rys. 3. Relacje między fundamentalnymi stałymi fizycznymi a podstawowymi jednostkami układu SI po redefinicji https://en.wikipedia.org/wiki/2019_redefinition_of_the_SI_base_units#/media/File:Unit_relations_in_the_new_SI.svg

W zredefiniowanym układzie SI nie narzuca się konkretnych realizacji wzorców jednostek, ale wymaga się, by po ich wprowadzeniu podstawowe stałe fizyczne przyjmowały w pomiarach wartości możliwie zbliżone do przyjętych odgórnie i całkowicie ustalonych wartości definicyjnych, przy czym:

• częstotliwość nadsubtelnego przejścia w atomach cezu 133 w niezaburzonym stanie podstawowym, Δν_Cs wynosi 9 192 631 770 Hz,
• prędkość światła w próżni c wynosi 299 792 458 m/s,
• stała Plancka h wynosi 6.626 070 15 × 10^-34 J s,
• ładunek elementarny e wynosi 1.602 176 634 × 10^-19 C,
• stała Boltzmanna k wynosi 1.380 649 × 10^-23 J/K,
• stała Avogadra N_A wynosi 6.022 140 76 × 10²³ mol^-1,
• skuteczność świetlna monochromatycznego promieniowania o częstotliwości 540 × 10¹² Hz, K_cd, wynosi 683 lm/W.

Jednostka masy została umownie powiązana ze stałą Plancka h (która jest podstawową stałą fizyki kwantowej), jednak w rzeczywistości konieczne było odniesienie jej również do dwóch innych stałych (prędkości światła c i częstości Δν_Cs cezowego zegara atomowego). Formalnie nowa definicja kilograma brzmi: „Kilogram, oznaczenie kg, jest to jednostka masy w SI. Jest ona zdefiniowana poprzez przyjęcie ustalonej wartości liczbowej stałej Plancka h wynoszącej 6,62607015⋅10^-34, wyrażonej w jednostce J·s, która jest równa kg⋅m²⋅s⁻¹, przy czym metr i sekunda zdefiniowane są za pomocą c i ∆ν_Cs”.

Co to jest i jak działa waga Watta-Kibble’a?

Światowa społeczność metrologii masy wybrała spośród kilku rozważanych realizacji nowego wzorca masy tzw. wagę Watta-Kibble’a [2]. Nazwa została nadana na cześć wynalazcy, Bryana Kibble’a z brytyjskiego National Physical Laboratory (NPL), który opracował pierwszą koncepcję już w 1975 roku (wówczas używał nazwy „waga Watta”). Jak każda współczesna waga laboratoryjna, jest ona zaprojektowana tak, by równoważyć ciężar masy testowej siłą elektrodynamiczną wytworzoną przez prąd elektryczny przepływający przez cewkę znajdującą się w zewnętrznym polu magnetycznym. Jego źródłem jest obwód magnetyczny złożony m.in. z silnych magnesów stałych lub z nieruchomego elektromagnesu. Ruchoma cewka, po przepuszczeniu przez nią prądu, staje się elektromagnesem siłownika o sile udźwigu proporcjonalnej do wartości zewnętrznego pola magnetycznego i natężenia prądu elektrycznego, którego wartość jest regulowana. Waga Watta-Kibble’a pracuje w dwóch trybach: w statycznym trybie ważenia i w dynamicznym trybie kalibracji (Rys. 4).

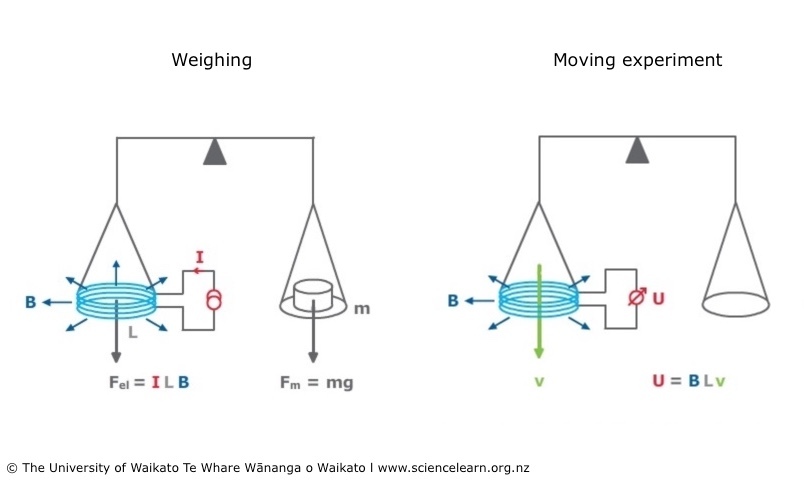
Rys. 4. Dwa tryby pracy wagi Watta-Kibble’a: tryb ważenia („Weighing”) i dynamiczny tryb kalibracji („Moving experiment”)
https://www.sciencelearn.org.nz/images/2288-weighing-experiment

Tryb ważenia (tryb siły)

W tym trybie masę testową umieszcza się na szalce przymocowanej do cewki. Masa wywiera siłę skierowaną w dół będącą jego ciężarem równym iloczynowi masy (m) i lokalnego przyspieszenia grawitacyjnego (g). Prąd przepuszczany przez cewkę jest tak regulowany, żeby siła elektrodynamiczna skierowana w górę dokładnie zrównoważyła siłę ciężkości. Gdy system osiągnie równowagę, rejestrowana jest wartość prądu. Siła elektrodynamiczna jest określona prostym równaniem F = I*B*L, gdzie I to natężenie prądu, B to indukcja pola magnetycznego, a L to długość drutu cewki. W stanie równowagi wartość siły F jest równa ciężarowi masy testowej m*g. Niestety te proste relacje nie wystarczają do realizacji wzorca masy, ponieważ wartość iloczynu B*L jest niezwykle trudna do bezpośredniego pomiaru z niezbędną dokładnością. Jednakże fizyka oferuje rozwiązanie tego problemu poprzez zastosowanie prawa indukcji Faradaya, które przewiduje powstawanie napięcia elektrycznego w przewodniku, gdy zmienia się strumień pola magnetycznego. Będzie ono dokładnie proporcjonalne do natężenia pola magnetycznego, prędkości cewki względem magnesu i długości jej uzwojenia. To jest podstawowa motywacja do zrealizowania drugiego trybu pracy wagi Watta-Kibble’a.

Tryb kalibracji (tryb prędkości)

W tym przypadku masa testowa jest usuwana z wagi, a prąd doprowadzany przez cewkę – wyłączany. Cewka jest następnie poruszana w polu magnetycznym z precyzyjnie kontrolowaną, stałą prędkością v. Mierzone jest powstające wówczas napięcie indukowane. Jego wartość z prawa indukcji Faradaya wynosi V = v*B*L. Kiedy to równanie zostanie połączone z formułą m*g = I*B*L wynikającą z równowagi sił w trybie ważenia, to wyeliminowane będą nieznane wielkości B i L oraz otrzymamy zależność I*V = m*g*ν, co sugeruje, że gdybyśmy w modzie kalibracji nie zdjęli masy i nie wyłączyli prądu, to, zgodnie z oczekiwaniami, moc elektryczna równałaby się mocy mechanicznej. Jako że obie wielkości wyraża się w watach, pierwotną nazwą opisywanego urządzenia była „waga Watta”. Jednakże najważniejszym, praktycznym wnioskiem wynikającym z ostatniego równania jest możliwość wyznaczenia masy:

m = I*V/g*v.

Wszystkie wielkości po prawej stronie tego równania można określić z niezwykłą precyzją: prąd i napięcie za pomocą kwantowych efektów elektrycznych, lokalne pole grawitacyjne – za pomocą ultraczułego urządzenia zwanego grawimetrem absolutnym, a prędkość cewki – poprzez śledzenie jej ruchu przy pomocy interferometrii laserowej (oferującej precyzję pomiaru położenia cewki z dokładnością do ułamka długości fali światła laserowego).

Jak fizyka kwantowa i stała Plancka zrewolucjonizowała metrologię masy?

Skoro realizacja nowego wzorca masy sprowadza się do pomiarów prostych wielkości elektrycznych oraz prędkości i przyspieszenia ziemskiego, to dlaczego temu wzorcowi przypisuje się w zredefiniowanym układzie SI związek ze stałą Plancka h? Generalnie stała Plancka została wprowadzona na początku XX wieku w celu prawidłowego opisu najmniejszych porcji energii E promieniowania, czyli fotonów poruszających się z prędkością światła c. Wzór Plancka przewiduje, że kwant energii wynosi E = h*ν, gdzie ν to częstotliwość fali promieniowania.

Gdyby foton posiadał masę, to na podstawie najbardziej znanego na świecie wzoru Einsteina o równoważności masy i energii E = m*c², można by w prosty sposób powiązać masę ze stałą Plancka, a metrologię masy sprowadzić do ultraprecyzyjnych pomiarów czasu (częstotliwości). Niestety fotony są cząstkami bezmasowymi, więc słynna formuła Einsteina ich nie dotyczy. Masą obdarzone są natomiast elektrony będące elementarnymi nośnikami ładunku elektrycznego odpowiedzialnymi za wszystkie zjawiska elektromagnetyczne zarówno makroskopowe, jak i w skali atomowej, gdzie obowiązują prawa fizyki kwantowej.

Prąd w wadze Watta-Kibble’a jest mierzony za pomocą rezystora wzorcowego w obwodzie. Wartość oporu elektrycznego można określić z precyzją około 1 części na miliard, odnosząc się do tzw. stałej von Klitzinga, która opisuje elementarny skok (kwant) oporu poprzecznego występujący przy zmianie pola magnetycznego w zjawisku znanym jako kwantowy efekt Halla. Napięcie elektryczne jest mierzone z dokładnością 1 części na 10 miliardów za pomocą tzw. efektu Josephsona, które przewiduje metrologicznie ścisłą proporcjonalność pomiędzy wartością napięcia przyłożonego do złącza nadprzewodnik-izolator-nadprzewodnik (złącze Josephsona) a częstotliwością generowanego promieniowania elektromagnetycznego.

W praktyce efekt Josephsona stanowi światowy standard kwantyfikacji napięcia, a kwantowy efekt Halla jest światowym wzorcem oporu elektrycznego, chociaż ani wolt, ani om nie jest podstawową jednostką układu SI. Samodzielne Laboratorium Elektryczności i Magnetyzmu Głównego Urzędu Miar w Warszawie od wielu lat dysponuje profesjonalnymi realizacjami obydwu wzorców (Rys. 5).

Rys. 5. Państwowe wzorce jednostki miary stałego napięcia elektrycznego (zdjęcie lewe: złącza Josepsona z instalacją kriogeniczną) i rezystancji (zdjęcia prawe: układ kriogeniczny do realizacji kwantowego efektu Halla) funkcjonujące w Głównym Urzędzie Miar w Warszawie od, odpowiednio, 2003 i 2016 roku
www.gum.gov.pl

Po połączeniu uprzednio wyprowadzonego wzoru do wyliczania masy testowanej w wadze Watta-Kibble’a ze wzorami opisującymi kwantowy efekt Halla i efekt Josephsona, otrzymujemy ścisłą proporcjonalność pomiędzy wartością masy m a wartością stałej Plancka h:

m = h*[n²/p]*[f_f*f_c]/[4*v*g],

przy czym n oznacza liczbę złącz Josephsona we wzorcu napięcia, p – numer „schodka” oporu w kwantowym efekcie Halla, f_f – częstotliwość promieniowania ze złącza Josephsona wykorzystywanego do pomiaru napięcia na oporze wzorcowym w obwodzie wagi w trybie ważenia (force mode), a f_c –  analogiczna częstotliwość odpowiadająca pomiarowi napięcia indukującego się w cewce wagi pracującej w trybie dynamicznym (calibration mode).

Jak wygląda realizacja wagi Watta-Kibble’a w BIPM (Sèvres)?

Konstruktorzy wagi Watta-Kibble’a w Międzynarodowym Biurze Miar w Sèvres pod Paryżem (Bureau International des Poids et Mesures, BIPM) zastosowali osiową, jednoramienną geometrię wagi Watta-Kibble’a (Rys. 6), co upraszcza konstrukcję, ale powoduje problemy z mechanicznym zrównoważeniem układu – w porównaniu do klasycznej, dwuramiennej geometrii wag mechanicznych. W celu utrzymania ciężaru ruchomego elementu osiowego wagi użyto kompensacyjnego komparatora masy. Geometria jednoosiowa umożliwia łatwe umieszczenie wagi w komorze próżniowej, przy czym zapewnienie próżni jest warunkiem koniecznym do prawidłowego funkcjonowania Watta-Kibble’a w trybie zarówno ważenia, jak i kalibracji.

Rys. 6. Realizacja wagi Watta-Kibble’a w BIPM (Sèvres)
https://www.bipm.org/en/mass-metrology/kibble-balance

Waga Watta-Kibble’a w BIPM odznacza się kilkoma innowacyjnymi cechami. Jedną z nich jest możliwość pracy symultanicznej łączącej w sobie elementy trybu ważenia i kalibracji. Kolejnym wyróżnikiem konstrukcji jest zoptymalizowany obwód magnetyczny wykorzystujący dwa wysokiej klasy magnesy samarowo-kobaltowe i jarzmo ze stopu Fe-Ni (bardziej miękkiego magnetycznie niż stal). Dzięki niemu osiągnięto dużą jednorodność radialną pola magnetycznego w szczelinie, jego relatywnie wysoką wartość (do 0,5 T)  perfekcyjną stabilność termiczną. Konstruktorzy testują też wykorzystanie siłowników elektrostatycznych do poruszania cewką (zamiast konwencjonalnych, krokowych silników elektromagnetycznych). Dzięki temu możliwe będzie uzyskanie wyjątkowej precyzji ruchu cewki i wyeliminowanie wpływu pól magnetycznych. Zaprojektowano również bardzo precyzyjny układ optyczny do śledzenia położenia i prędkości cewki. Wykorzystano do tego celu  najbardziej zaawansowane interferometry heterodynowe i lasery o wysokiej stabilności emisji. Wagi Watta-Kibble’a zostały skonstruowane w wielu narodowych instytutach metrologicznych na świecie, a obecnie BIPM koordynuje nową fazę procesu dyseminacji kilograma poprzez proces komparacji międzylaboratoryjnych [3].

Jak oferta firmy RADWAG ułatwia transfer wzorców masy po redefinicji?

Wprowadzenie nowego wzorca masy w postaci wagi Watta-Kibble’a nie wyeliminowało potrzeby zastosowania materialnych artefaktów jako wzorców wtórnych i odważników kalibracyjnych. Wzrosły jednak wymogi odnoszące się do zapewnienia spójności masy w procesie transferu wzorców i ich dyseminacji.

Firma RADWAG wyszła naprzeciw temu zapotrzebowaniu i skonstruowała automatyczny, próżniowy komparator masy AVK-1000 (Rys. 7.) o obciążeniu maksymalnym 1 kg, z działką elementarną 0,1 μg. Urządzenie oferuje prowadzenie pomiarów w próżni o wartości 10^-6 mbar lub w atmosferze gazów szlachetnych i neutralnych. Próżnia lub zapewnienie stałego ciśnienia eliminuje błędy komparacji masy związane z niedoskonałym kompensowaniem siły wyporu. Urządzenie przeznaczone jest do komparacji tradycyjnych, cylindrycznych wzorców stalowych (o średnicy 22-95 mm) i kul krzemowych (o średnicy 40-100 mm), które były brane pod uwagę jako alternatywne (wobec wagi Watta-Kibble’a) wzorce masy po redefinicji układu SI, a ostatecznie zostały uznane za najlepszy, praktyczny wzorzec gęstości. Komparator próżniowy AVK-1000 wyposażony jest w system przenoszenia wzorca LOAD LOCK. Dzięki niemu możliwa jest wymiana lub dołożenie artefaktów bez konieczności zmiany atmosfery wewnątrz komory głównej komparatora, co skraca czas pomiarów o 90%.

Automatyczny próżniowy komparator masy AVK-1000 pracuje od kilku lat w Samodzielnym Laboratorium Masy Głównego Urzędu Miar w Warszawie. Precyzja pomiarów, jaką oferuje to urządzenie i zastosowane w nim rozwiązania technologiczne, mogą stanowić w przyszłości dobry punkt wyjścia do realizacji polskiego projektu wagi Watta-Kibble’a [4].

Rys. 7. Automatyczny próżniowy komparator masy AVK-1000 produkcji firmy RADWAG zainstalowany w Samodzielnym Laboratorium Masy Głównego Urzędu Miar w Warszawie

W jaki sposób po redefinicji układu SI firma RADWAG stała się światowym liderem metrologii masy w zakresie nano?

RADWAG, jako pierwsza firma na świecie, wprowadziła na rynek automatyczny nano-komparator masy o symbolu NANO.AK-4/500N (Rys. 8) o rekordowej dokładności odczytu 10 ng i udźwigu maksymalnym 510 mg [5]. Komparator ten cechuje się znacznie lepszymi charakterystykami niż inne urządzenia tego typu dostępne na rynku i stanowi przełom w światowej metrologii masy. Ulepszenia siłownika i cewki [6] zminimalizowały wpływ warunków otoczenia na wyniki pomiarów, szczególnie w przypadku gradientu wilgotności powietrza. Odchylenie standardowe wyliczone na podstawie 20 powtórzonych cykli komparacji ABBA wyniosło 38 ng [6] w przypadku odważnika 2 mg. Jest to obecnie najlepsza dostępna w metrologii małych mas powtarzalność pomiarów. Wyniki te potwierdziły jednoznacznie, że innowacyjna konstrukcja komparatora masy NANO.AK-4/500N umożliwia kalibrowanie odważników z dokładnością nanogramową.

Rys. 8. Pierwszy na świecie automatyczny nano-komparator masy (NANO.AK-4/500N, RADWAG)

Pojawienie się pierwszego na światowym rynku komparatora masy o rozdzielczości 10 ng pozwala na walidowanie materialnych wzorców masy do kalibracji mikrowag laboratoryjnych stosowanych w wielu gałęziach przemysłu, laboratoriach wzorcujących i w badaniach naukowych w ramach różnych dyscyplin.

Typowym obszarem zastosowań jest kalibracja mikrowag używanych w przemyśle farmaceutycznym do przygotowywania nowych receptur. Bardzo istotnym przykładem zastosowań są wszelkie badania fizykochemiczne materiałów (analityka chemiczna, spektroskopia), w których mierzone wielkości fizyczne i zawartości pierwiastków są odnoszone do precyzyjnie wyznaczonej masy. Szczególnie ważną kwestią jest kalibracja grawimetryczna mierników pyłu zawieszonego PM10 i PM2.5 mająca kluczowe znaczenie w monitoringu środowiskowym. Innym obszarem zastosowań jest nowoczesny przemysł elektroniczny i mechatroniczny, gdzie szczególnie ważną kwestią staje się m.in. kalibracja mikro- i nanosiłowników oraz sensorów. 

Skonstruowany nano-komparator wpisuje się w światowy system metrologii masy, który po rewolucyjnych zmianach układu SI z roku 2018 zaleca skonstruowanie niezależnego, niematerialnego wzorca na zakres małych mas [2, 4, 7] w postaci miniaturowej wagi Watta-Kibble’a.

Literatura:

[1] E. Gibney, „Largest overhaul of scientific units since 1875 wins approval”, NATURE NEWS, 16 November 2018, https://www.nature.com/articles/d41586-018-07424-8

[2] S. Schlamminger, D. Haddad, „The new International System of Units – The Kibble balance and the kilogram”, Comptes Rendus Physique 20 (2019) 55-63, https://doi.org/10.1016/j.crhy.2018.11.006

[3] S. Davidson, M. Stock, „Beginning of a new phase of the dissemination of the kilogram”, Metrologia 58 (2021) 033002 (4pp), https://iopscience.iop.org/article/10.1088/1681-7575/abef9f

[4] T. Szumiata, M. Dobieszewski, A. Hantz, W. Wiśniewski, J. Szutkowski, A. Podgórni, M. Janeczko, „Analiza strategiczna polskiego projektu wagi Kibble’a”, METROLOGIA I PROBIERNICTWO, Biuletyn GUM nr 1 (22)/2019, https://www.gum.gov.pl/ftp/pdf/Biuletyn/Artykuly/Analiza_strategiczna_polskiego_projektu_wagi_Kibble___a.pdf

[5] Broszura produktowa (2021) z oferty firmy RADWAG: „Automatyczny nano komparator masy NANO.AK-4/500”, https://radwag.com/pl/automatyczny-nano-komparator-masy-nano-ak-4-500,w1,R6X,110-106#4

[6] M. Solecki, T. Szumiata, M. Rucki, „A new design of an automatic mass comparator with the resolution of 10 ng for calibration of masses below 2 mg” (2021), artykuł wysłany do Precision Engineering (Elsevier)

[7] L. Chao , F. Seifert, D. Haddad, J. Stirling, D. Newell, S. Schlamminger, „The design and development of a tabletop kibble balance at NIST”, IEEE Transactions on Instrumentation and Measurement, 68 (2019) 2176-2182, https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=8672111